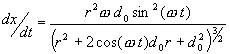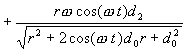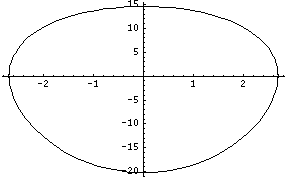Most shapers that you are likely to come across in an amateur's workshop will be column shapers like the one pictured above. The motor, through a combination of belts, pulleys and gears, ultimately turns the large bull gear. Pictured above we see the rocking arm that pivots at point P0 is pushed by the offset pin in the bull gear at point P1. By setting the position of this point you determine the length of your shaper's stroke. The top of the rocking arm at point P2 supplies the forward and backward motion of your ram through the link to point P3. The correct direction is for the motor to move the bull gear clockwise (in the drawing above) such that the top of the bull gear is always moving towards the front of the shaper.
This motion of the eccentric pin at point P1 will cause the ram to move forward on the cutting stroke more slowly than when it is retracting. The assumption is that you need all the power available to cut the steel but on the return stroke you can trade off power for speed and increase production. The reality is less dramatic. On modest stroke lengths there is very little difference in speed between the power stroke and the retract stroke. If you set your shaper on its lowest speed you will be hard pressed to notice the difference. But on the maximum length stroke the ram does retract noticeably faster then the power stroke.
If you run the motor backwards it still works fine. This brings up an interesting question about old machinery. Here we have a shaper that has been running for 30 years in the same direction. At the beginning of the power stroke when the tool bit first hits the steel there is one or two teeth in the bull gear that do all the work. This is the most important part of the shaper to check if you are looking at a used shaper. Make sure there are no teeth missing from the bull gear. But if we reverse the motor and run the bull gear backwards will it spread the wear out more evenly and last longer or will it stress some poor gear tooth in a way that it had never been stressed before and cause a premature failure? Think about it and maybe we can have a show of hands at the next meeting.
Jay Stryker (one of our club members who is a shaper expert) asked the question in another way.
“Shapers were designed for slow speed cutting on cast iron. For aluminum, this is too slow. Is it OK to use a mechanical (bull-geared) shaper running in reverse to get the higher speed of the rapid retract for the forward stroke in order to cut aluminum.? Would this wear the linkage or cause some mechanical problem? The advantage is that one could use the "ordinary speeds", instead of running the shaper at its highest speed.” (I never imagined when I asked for questions that I would get the leading experts asking tough questions.)
I thought about it quite a bit and the short answer is no. I don't think wear would be a problem as discussed above but I don't think you would realize any speed advantage. Since the speed difference is only significant on long strokes and since the shaper slows down at the beginning and ending of each stroke the speed difference is only over a very short length in the middle of the part being machined.
And I can prove it! If you don't like math now is a good time to skip to the next article in the news letter.
Point P0 is the pivot point of the rocking arm and will be considered the origin for all values. Point P1 as the bull wheel turns travels to the right and left as a function of the sine of the angle of the bull wheel. If we consider the ram stroke as the X direction and the up and down motion of the offset pin as the Y direction then point P1 moves around in a circle and any given point will be represented as X1 and Y1. Point P2 will be at X2 and Y2. And lastly point P3 (which is what we really care about) will be at X3 and Y3.
r = the radius of the offset Pin P1.
d0 = the distance from P0 to the center of the bull gear (a constant).
d1 = the distance from P0 to P1.
d2 = the distance from P0 to P2 (a constant).
h = the distance from P2 to P3 (a constant).
X1 = r sin(wt)
Y1 = d0 + r cos(wt)
We also know that the point at the end of the rocking arm P2 will be in a straight line with P1 so the slope of the line from P0 to P1 is always equal to the slope of the line from P0 to P2. The important idea is that, since points P0, P1, and P2 are always in a straight line, we know that:
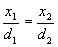 Solving for x2 we get
Solving for x2 we get

Both ratios are equal to the sine of the angle that the arm makes with the vertical (if that helps).
d1 is the hypotenuse of the right triangle from point P0 to P1 with the bull gear centered to P1 with the bull gear turned to any angle. Using the Pythagorean theorem we get:
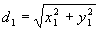
Substituting in the values for x1 and y1 earlier we get:
Squaring both terms we get:
Moving the two r2 terms to the left we get
We factor r2 out of the two terms on the left to become:
Using the trigonometric identity
Or simply
Now substituting the value for d1 above and the value for x1 that we had long ago we get:
This gives the position of P2, not P3 as desired. But it turns out that they are almost identical in their relative X position when calculated.
However, we can get the exact answer, since we know that:
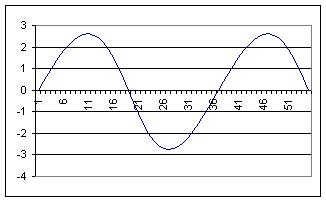
This was using data from my 7 inch Rhodes shaper with d0 = 10”, d2 = 16.6”, and r = 1.625” giving a stroke of 5”.
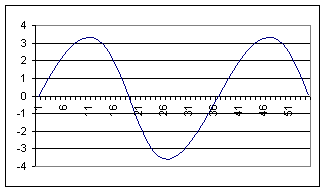
You will notice that it looks almost symmetrical. This shows that the retract cycle is nearly equal to the power stroke. If I increases the radius of the eccentric pin on the bull gear to 2.1” the plot of the tool becomes slightly distorted to reflect the slow forward motion and rapid retract as follows:
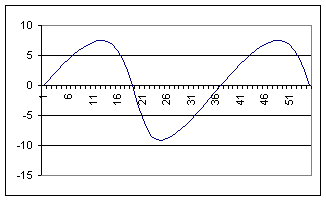
Unfortunately it is still difficult to see any real change and this is currently at a 7-inch stroke – the max my poor little Rhodes can handle. However the software doesn't know the real diameter of my bull gear so here is what it would look like if I could increase the radius of the offset pin to 5 inches giving a stroke of 19 inches:
This exaggerated view shows slow power stroke and the rapid retract. The slope of the waveform at any point represents the velocity.
I knew that the tool path was following a sine function but to allow for the extra geometry of the rocking arm and the link I had to enlist the aid of my friend, colleague, and math mentor Michael Tsuk. Michael developed the formulas and led me thru the proofs and helped me simplify the steps to bite size pieces that I could understand. In addition he entered the data into Mathematica and had prototype waveforms proving the validity before I created a Microsoft Excel spreadsheet from which I captured the above graphs.
The next step (Oh no there's more!) is to recognize that what we really care about is not the X position over time but the velocity of the tool which is the slope of the plot. To see this we could take little bites of the X and Y values from the spreadsheet and make a graph of the values of all the individual slopes. This would give us relative velocities but not in any measurable units. To accurately graph the actual velocity of the tool path in real units we need to find the derivative of the previous formula. For this we need to leave Excel and go into Mathematica.
The formula for derivative of the tool position over time gives us the answer to tool velocity in inches per second.
This yields the following graph where the large sine wave is the velocity of the tool in inches per second and the small sine wave is the previously plotted tool position varying from plus and minus 2.5 inches for a 5 inch stroke. We are assuming here a shaper speed of 1 stroke per second. If you were running at 2 strokes per second you could simply double the velocity values.
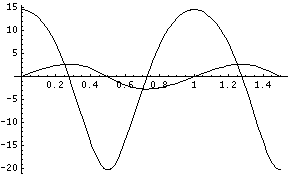
What we would like to know from the above graph is specific values of velocity at specific positions on the tool position. For instance we would like to know the velocity at the center of the work piece and at each end. It is a little difficult to see on this scale but if we create a parametric plot from Mathematica we get the following:
Now we are getting close to the truth. The top of the plot is the power stroke with a maximum velocity of 14.5 inches per second. The bottom shows the return stroke at 20 inches per second. With a 7 inch shaper set up with a 5 inch stroke on a 4.5 inch work piece the velocity near the end of the work piece at the –2 and +2 inch marks would be approximately 10.5 inches per second on the power stroke and approximately 12 inches per second on the return stroke.
So if you run your motor backwards although the speed would increase from 14.5 to 20 inches per second in the center of the work piece it would only increase from 10.5 to 12 inches per second near the ends of the work piece. Not enough change to expect for any increase in finish quality. If you were to increase the stroke to the maximum (7 inches in this case) you would have even less gain in tool speed near the ends of the work piece.
OK – I promise – no more shaper math J
Keep sending email with questions and interesting shaper stories.
My email address is KayPatFisher@gmail.com.

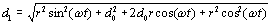


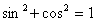 we can simplify the equation to:
we can simplify the equation to:
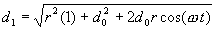

Our original formula for x2 was:
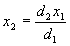
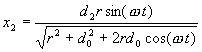

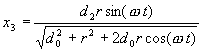
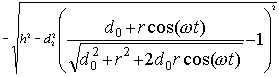
Substituting in known values and varying wt for one cycle we can plot the tool bit travel in X over time as follows: